반응형
4주차 계획
- 커리큘럼
- 일정 : 7/22 ~ 7/28
- 진도 : Chapter 04
- 기본 미션 : p. 279의 확인 문제 5번 풀고 인증하기
- 추가 미션 : Ch.04(04-1)에서 배운 8가지 기술통계량(평균, 중앙값, 최솟값, 최댓값, 분위수, 분산, 표준편차, 최빈값)의 개념을 정리하기
미션
기본 미션
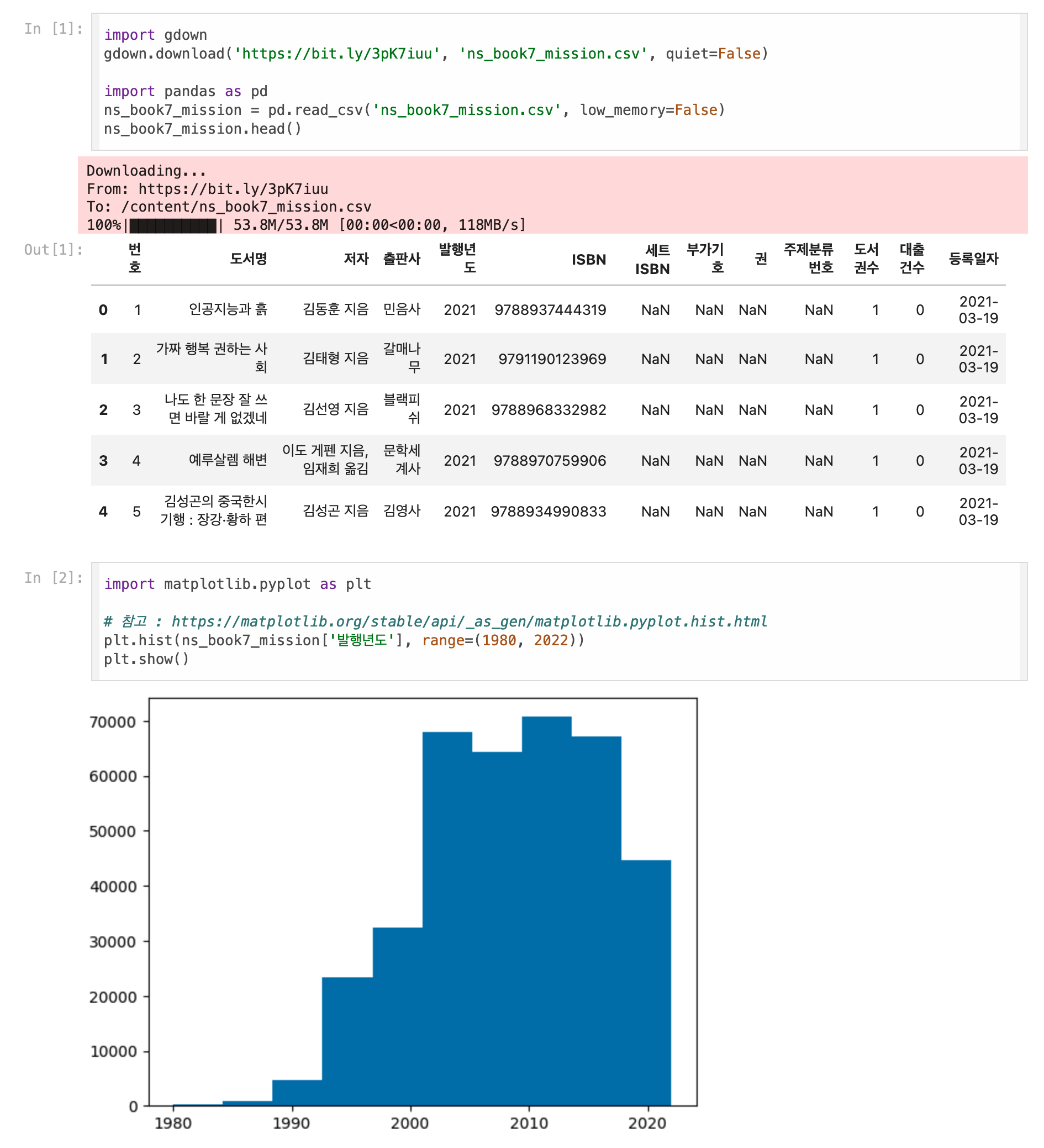
- ns_book7 남산도서관 대출 데이터에서 1980년~2022년 사이에 발행된 도서를 선택하여 다음과 같은 '발행년도' 열의 히스토그램을 그려보세요
추가 미션
Ch.04(04-1)에서 배운 8가지 기술통계량(평균, 중앙값, 최솟값, 최댓값, 분위수, 분산, 표준편차, 최빈값)의 개념을 정리하기
- 평균
- 판다스 메서드 : mean()
- 기술통계 표시 : maen
- 중앙값
- 전체 데이터를 순서대로 늘여놓았을 때 중앙에 위치한 값 = 50% 위치의 값
- 판다스 메서드 : median()
- 기술통계 표시 : 50%
- 최소값
- 판다스 메서드 : min()
- 기술통계 표시 : min
- 최댓값
- 판다스 메서드 : max()
- 기술통계 표시 : max
- 분산
- 평균으로부터 데이터가 얼마나 퍼져있는지 나타내는 통계량
- 수식 기호 : Var(𝑥), 𝜎2, 𝑠2
- 수식𝑠2=∑𝑛=𝑖𝑛(𝑥𝑖−𝑥¯)2𝑛
- 데이터의 각 값에서 평균을 뺀 다음 제곱한 후 (평균처럼) 샘플 개수로 나누어 구한다.
- 판다스 메서드 : var()
- 기술통계 표시 : X
- 표준편차
- 분산에 제곱근을 한 것
- 수식 기호 : 𝑠
- 수식𝑠=∑𝑛=𝑖𝑛(𝑥𝑖−𝑥¯)2𝑛
- 판다스 메서드 : std()
- 기술통계 표시 : std
- 최빈값
- 판다스 메서드 : mode()
- 기술통계 표시 :
Chapter 04. 데이터 요약하기
- 학습목표
- 전체 데이터를 숫자로 요약하는 방법을 배운다.
- 데이터 분포를 살펴보고 그래프를 통해 이해하는 방법을 알아본다.
04-1. 통계로 요약하기
- 기술통계(descriptive statistics)
- 자료의 내용을 압축하여 설명하는 방법
- 요약 통계(summary statistics)
- 평균, 표준편차 등
- 탐색적 데이터 분석(exploratory data analysis)
- 데이터 시각화를 아우르는 데이터 분석 방법
기술통계 구하기
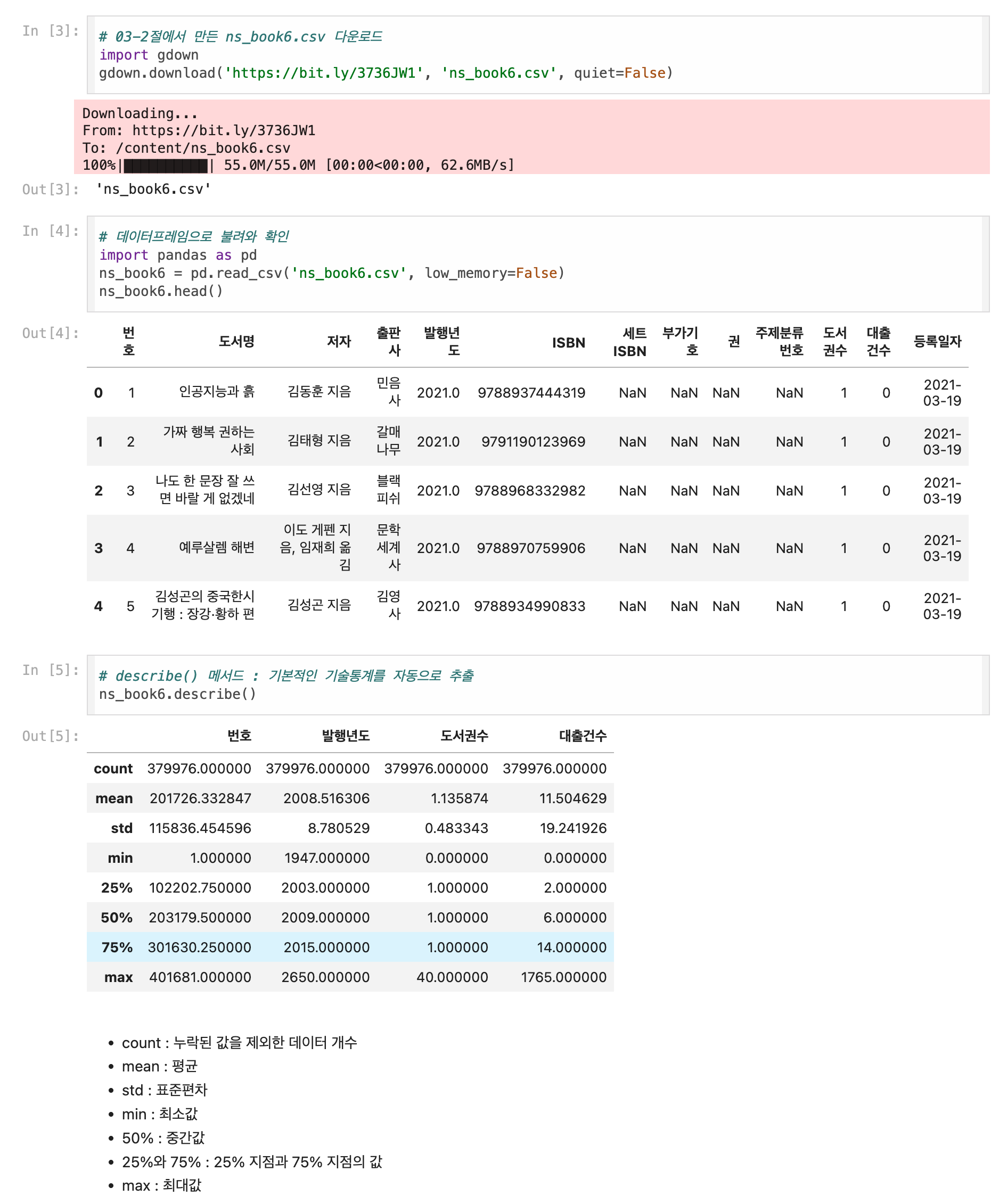
- 판다스의 describe() 메서드로 기술통계를 확인할 수 있다.

평균 구하기
- 메서드 : mean()

중앙값 구하기
- 중앙값(median)
- 전체 데이터를 순서대로 늘어 놓았을 때 중앙에 위치한 값 = 50% 위치의 값
- 메서드 : median()

최소값, 최대값 구하기
- 최소값 메서드 : min()
- 최대값 메서드 : max()

분위수 구하기
- 분위수(quantile)
- 데이터를 순서대로 늘어 놓았을 때, 이를 균등한 간격으로 나누는 기준점
- 이분위수 : 전체 데이터를 두 구간으로 나눔 - 50%
- 사분위수 : 전체 데이터를 네 구간으로 나눔 - 25%(제1사분위수), 50%(제2사분위수), 75%(제3사분위수)
- 메서드 : quantile()
- 보간(interpolation)
- 중간값 계산 방법을 결정
- quantile() 메서드의 파라미터로 전달 가능
- linear(기본값)
- midpoint : 두 수 사이의 중앙값 사용
- nearest : 두 수 중에서 가까운 값 사용

백분위 구하기

분산 구하기
- 분산(variance)
- 평균으로부터 데이터가 얼마나 퍼져있는지 나타내는 통계량
- 수식 기호 : Var(𝑥), 𝜎2, 𝑠2
- 수식𝑠2=∑𝑛=𝑖𝑛(𝑥𝑖−𝑥¯)2𝑛
- 데이터의 각 값에서 평균을 뺀 다음 제곱한 후 (평균처럼) 샘플 개수로 나누어 구한다.
- 메서드 : var()
- 특징
- 분산은 데이터가 평균에서 얼마나 퍼져있는지 나타내는 값이기 때문에 결과값만 보고 값지 큰지 작은지 판단하기 어렵다.
- 분산은 제곱을 했기 때문에 평균에서 멀어질수록 값이 급격하게 커지며, 해석하기 어렵다.
- 이를 보완하기 위해 분산에 제곱근을 취한 표준편차를 사용한다.

표준편차 구하기
- 표준편차(standard deviation)
- 분산에 제급근을 한 것
- 수식 기호 : 𝑠
- 수식𝑠=∑𝑛=𝑖𝑛(𝑥𝑖−𝑥¯)2𝑛
- 메서드 : std()

최빈값 구하기
- 최빈값(mode)
- 메서드 : mode()

데이터프레임에서 기술통계 구하기
- numeric_only=True로 매개변수를 지정하면, 기술통계를 구할 때 수치형 열만 모아서 연산한다.

04-2. 분포 요약하기
- 산점도(scrapper plot), 히스토그램(histogram), 상자 수염 그림(box-and-whisker plot) 배우기
산점도 그리기
- 산점도
- 데이터를 화면에 뿌리듯 그리는 그래프
- 두 변수(variable) 혹은 두 가지 특성(feature) 값을 직교 좌표계에 점으로 나타내는 그래프
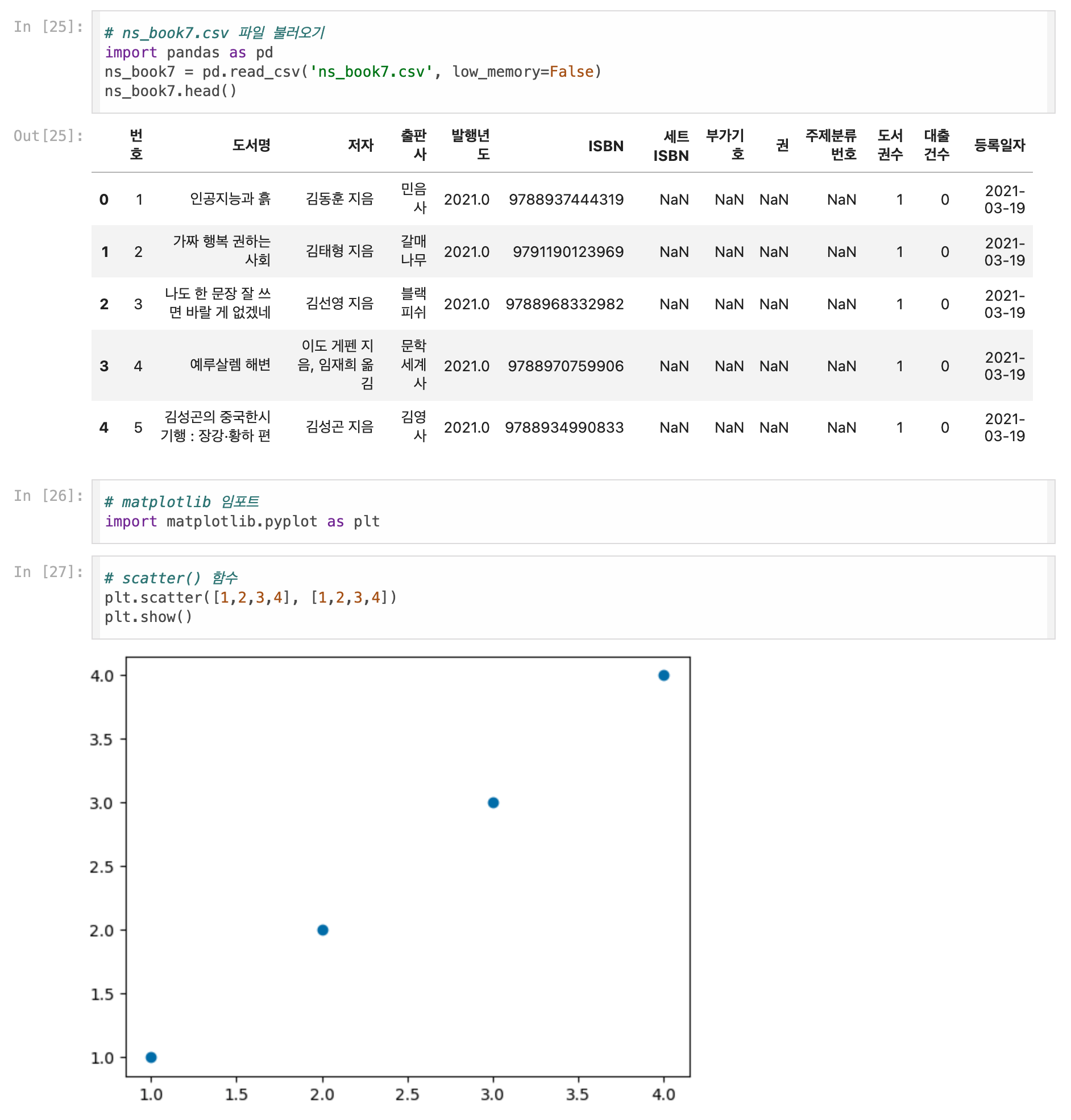
- scatter() 함수
- 산점도를 그리는 함수
- show() 함수
- 그래프를 출력하는 함수


히스토그램 그리기
- 히스토그램
- 수치형 특성의 값을 일정한 구간(bin)으로 나누어 구간 아네 포함된 데이터 개수를 막대 그래프로 그린 것
- 하나의 특성에 대한 분포를 확인하기 좋다.
- 도수(frequency) : 구간 안에 속한 데이터 개수
- 도수 분포표(frequency table) : 히스토그램에 나오는 구간과 도수를 표로 요악한 것
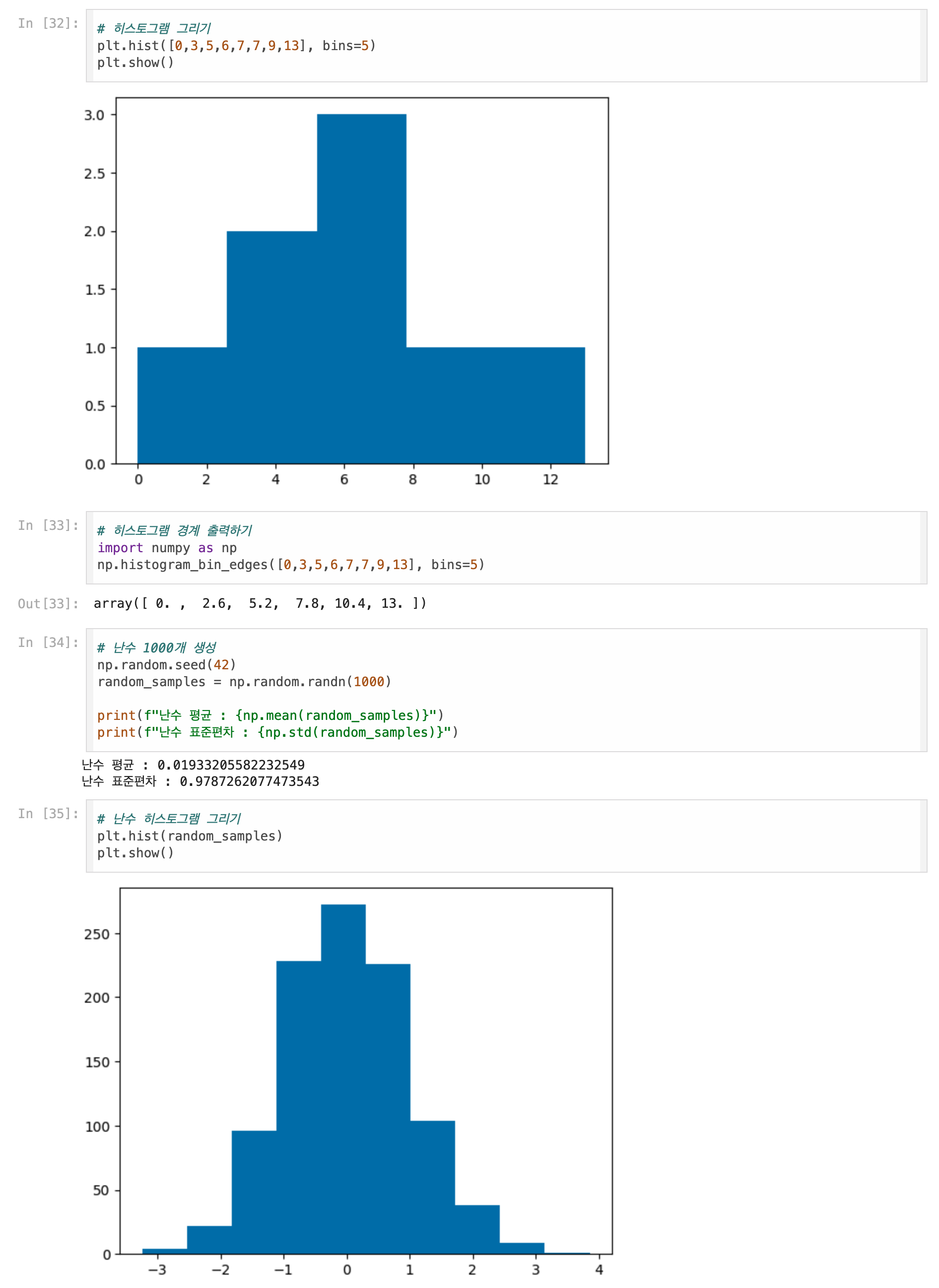
- hist() 함수
- 히스토그램을 그리는 함수
- 1차원 데이터를 입력받아 그리고, 기본적으로 10개의 구간으로 나눈다.
- bins 매개변수로 구간을 지정할 수 있다.
- 구간 조정하기
- 한 구가의 도수가 너무 큰 경우 > 다른 구간에서 도수가 표시되지 않음
- y축을 "로그 스케일(log scale)"로 바꿔 해결 가능
- 로그 스케일(log scale) : 로그 함수 적용



상자 수염 그림 그리기
- 상자 수염 그림
- "최소값, 세 개의 사분위수, 최댓값" 총 5개의 숫자를 사용해 데이터를 요약하는 그래프를 그린다.
- 상자 수염 그림 그리는 방법
- 사분위수 계산하고, 25%와 75% 지점을 밑면과 윗면으로 하는 직사각형 그리기
- 중간값(50% 지점) 지점에 수평선 긋기
- 사각형의 밑면과 윗면에서 사각형의 높이의 1.5배만큼 떨어진 거리 안에서 가장 멀리 있는 샘플까지 수직선을 긋는다.
- 이 수직선 밖에서 최소값과 최대값까지 데이터를 점으로 표시한다. 이 영역의 데이터를 이상치(outlier)라고 한다.
- IQR(interquartile range)
- 제1사분위수(25% 백분위수)와 제3사분위수(75% 백분위수) 사이의 거리
- boxplot() 함수
- 상자 수혐 그림을 그리는 함수



반응형